Chance de ganhar na mega sena

Já pensou em apostar na mega sena?
As chances de ganhar na mega sena são muito poucas.

Os ganhadores são 1 / 50. 063. 860.

Uau! Isso que é sorte!

Googol Plex

Você sabia que o maior número com nome que existe é o Googol Plex?
Como se calcula o Googol Plex?

Googol Plex é 10 elevado a um Googol. Mas o que é um Googol?

Um Googol é 10 elevado a 100.

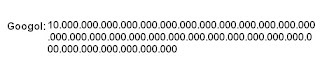
Portanto um Googol Plex é 10 elevado a 10 elevado a cem:




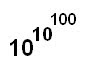
A soma de todas as partículas existentes no Universo é igual a 10 elevado na 80 (inferior ao Googol Plex).
Que número grande, não?

Até agora, sabemos que escrever um Googol Plex é impossível. Mesmo começando a escrever desde o Big Bang não teria tempo de finalizar a escrita do Googol Plex.

Outra forma de calcular potências

Pitágoras descobriu outra forma de calcular o quadrado de um número através da soma de números ímpares.
N² é igual a soma dos N primeiros números ímpares. Ãhn?

Veja o exemplo:
6² = 1 + 3 + 5 + 7 + 9 + 11
6² = 36

Legal, né?

Números Ascendentes

Um número natural é chamado de ascendente é se cada um dos seus algarismos é estritamente maior do que qualquer um dos algarismos colocados à sua esquerda:
Exemplo:
2589
O 9 é maior que o 8, que é maior que 0 5, que é maior que o 2.
Portanto é um número ascendente!

Número Mágico

1089 é conhecido como número mágico.

Como assim?
Escolha qualquer número de três algarismos.

Exemplo: 369
Agora, escreva-o de trás para frente: 963
Subtraia o número maior pelo menor: 963 - 369 = 594

Então, inverta o resultado: 495
Some os dois: 594 + 495 = 1089

Interessante, não?

Obs.: O operação somente resultará no número 1089 se, na subtração, o resultado não for um número palíndromo.

Como podemos calcular a velocidade de um carro após o acidente?

A fórmula usada é:




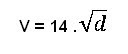
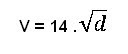
V = velocidade, d = distância das marcas dos pneus

Se as marcas tiverem a distância de 25 metros, qual seria a velocidade do automóvel?
Assim substituímos "d" por 25. A raiz quadrada de 25 é 5; então:
v = 14 . 5
v = 70

A velocidade do carro era 70 km/h .
Legal, né? Essa é a fórmula usada pela polícia técnica para determinar a velocidade do automóvel, após os acidentes de trânsito.

Teorema de Pitágoras

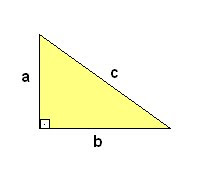
A soma dos quadrados dos catetos é igual ao quadrado da hipotenusa. O QUÊ?

Catetos são o lado e a base do triângulo retângulo (triângulo com um ângulo reto) e a hipotenusa é a diagonal. Na imagem ao lado podemos ver os dois catetos ("a" e "b") e a hipotenusa ("c").

Agora veja:

= (a² + b²) = c²

Substituindo por números:

se a = 3, b = 4, c = ?

3² + 4² = c²

9 + 16 = c²

25 = c²

Agora para saber o valor apenas de c devemos tirar a raiz quadrada dos termos:

5 = c

Trinômios Quadrados Perfeitos

=> Quadrado da soma de de dois termos:

O quadrado do primeiro termo, mais duas vezes o primeiro termo vezes o segundo termo, mais o segundo termo ao quadrado.
Parece difícil, não? Mas é muito simples! Veja:
= (a + b)²
* simplificando essa conta temos:
= (a + b) . (a + b)
*agora devemos multiplicar todos os termos (a . a, a . b, a . b e b . b):
= a² + a . b + a . b + b²
*então some o que for preciso:
a² + 2ab + b²
* isso é igual a (primeiro termo)² + 2 . (primeiro termo) . (segundo termo) + (segundo termo)²
primeiro termo = a / segundo termo = b

=> Quadrado da diferença de dois termos:

O quadrado do primeiro termo, menos duas vezes o primeiro termo vezes o segundo termo, mais o segundo termo ao quadrado.
Veja:
= (a - b)²
*simplificando...
= (a -b) . (a - b)
*multiplique todos os termos (a . a, a . -b, a . -b, -b . -b) :
= a² - ab - ab + b²
*some...
= a² - 2ab + b²
* isto é igual a: (primeiro termo)² - 2. (primeiro termo) . (segundo termo) + (segundo termo)²

=> Produto da soma pela diferença de 2 termos:

O quadrado do primeiro termo, menos o quadrado do segundo termo.
Veja:
= (a + b) . (a - b)
*multiplique todos os termos ( a . a, a . -b, a . b, b . -b):
= a² - ab + ab - b²
*subtraia...
= a² - b²
* isto é: (primeiro termo)² - (segundo termo)²